In my previous post, I implemented a simple parser for boolean expressions in ARM’s architecture specification language. Unfortunately, the parser I initially wrote using nom did not take operator precedence into account. To recap, with the logic I implemented in the last post the expression, op1 == '000' && CRn == '0111', would parse into an AST that resembles the following:

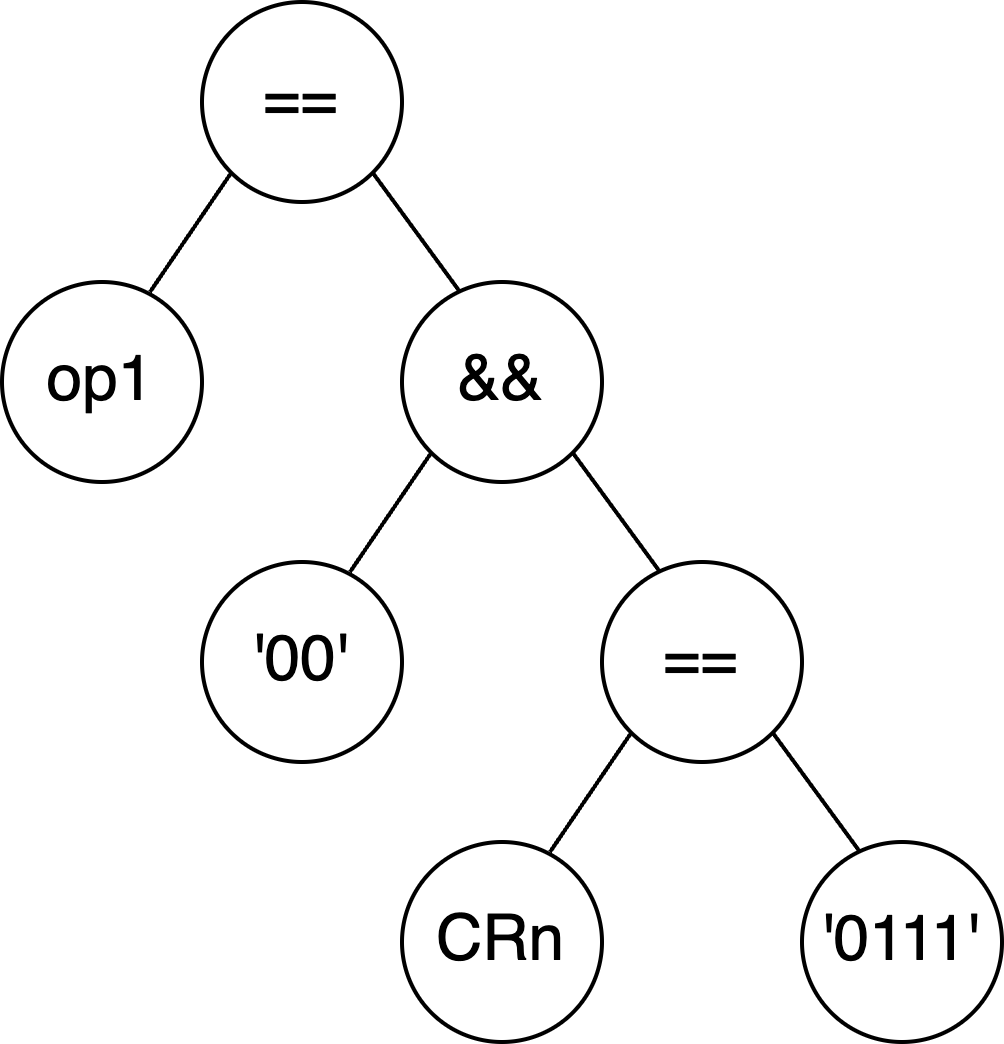
We can also describe the precedence here using parenthesis:

(op1 == ('000' && (CRn == '0111')))

This is clearly not right. In reality, we want the && operator to have a higher precedence than the equality operator so that we can end up with an AST like so:

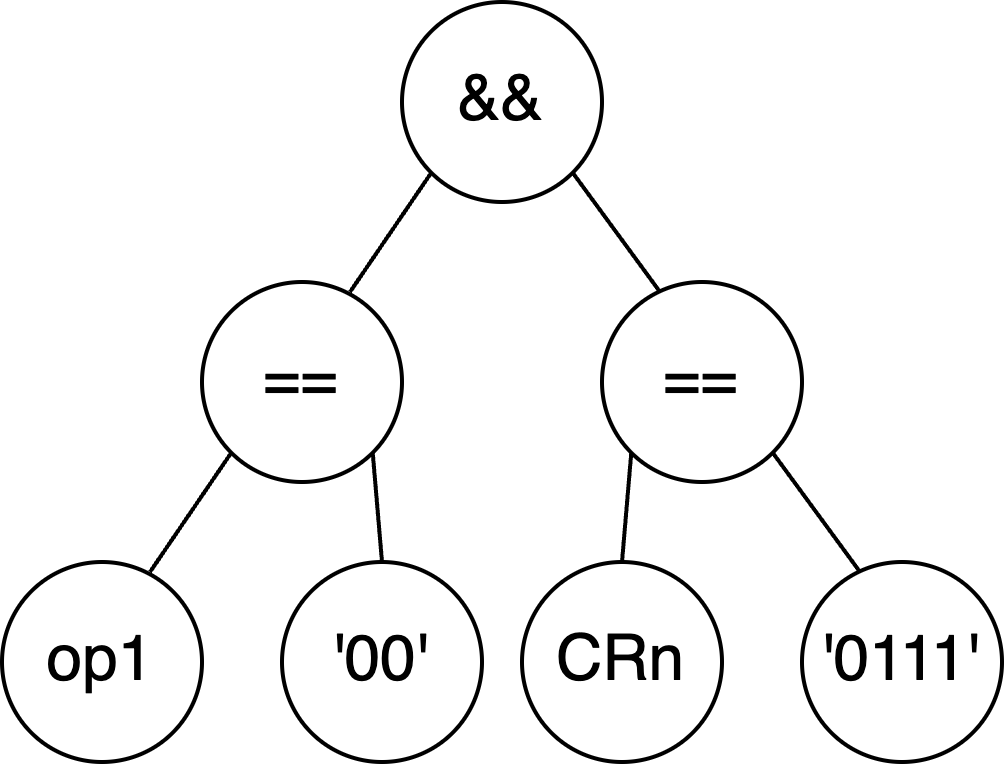
Which would reflect the following precedence:

(op1 == '00') && (CRn == '0111')

To accomplish this we need to keep precedence in mind while parsing. As with most things related to language parsers, this is a heavily researched topic and several algorithms exist for accomplishing this. After reading up on them, I decided that the easiest path forward for now would be to implement precedence climbing. Both the wikipedia article for operator-precedence parser and Eli Bendersky’s article on precedence climbing proved invaluable in my endeavors and I highly recommend Eli’s blog post in particular for developing a deeper understanding of these algorithms. In my blog post, I want to focus on implementing this particular algorithm in the context of the nom parser-combinator library.

Stateful parsing with nom

The basic idea of the precedence climbing algorithm is that you assign a precedence score to each operator in your grammar. While parsing expressions, if you find an operator with a lower precedence you return early. This allows us to group operations of higher precedence together before continuing to parse an expression.

parse_expression(lhs, min_precedence)
    lookahead := peek next token
    while lookahead is a binary operator whose precedence is >= min_precedence
        op := lookahead
        advance to next token
        rhs := parse_primary ()
        lookahead := peek next token
        while lookahead is a binary operator whose precedence is greater
                 than op's, or a right-associative operator
                 whose precedence is equal to op's
            rhs := parse_expression_1 (rhs, precedence of op + (1 if lookahead precedence is greater, else 0))
            lookahead := peek next token
        lhs := the result of applying op with operands lhs and rhs
    return lhs

The nom crate doesn’t really have built-in support for passing state around. Each combinator should be a stateless parser that returns a parsed result type. By default nom supports &str and &[u8] as valid input types, however users can define their own custom types by implementing the required set of traits.

In that case, we can build our own custom input type that carries with it some state. In our case, that state would be the current minimum precedence.

#[derive(Clone, Debug)]
pub struct Span<'a> {
    pub input: &'a str,
    pub min_precedence: u32,
}

There are quite a few traits we have to implement but we can mostly use the ones implemented by the nom crate for the &str type. These traits provide the basic capabilities needed by the built-in combinators in nom.

Once we have our custom input type, implementing the precedence climbing algorithm within nom is straightforward.

pub fn expr(code: Span) -> IResult<Span, Expr, Error<Span>> {
    let (i, mut lhs) = term(code)?;
    let mut current = i;
    loop {
        let (i, op) = match peek(operator)(current) {
            Ok(res) => res,
            Err(nom::Err::Error(e)) => { current = e.input; break; },
            Err(e) => return Err(e),
        };
        if precedence_for(op) < i.min_precedence {
            current = i;
            break;
        }
        let (mut i, op) = operator(i)?;
        let prev_precedence = i.min_precedence;
        i.min_precedence = precedence_for(op) + 1;
        let (mut i, rhs) = expr(i)?;
        i.min_precedence = prev_precedence;
        lhs = build_expr(op, lhs, rhs);
        current = i;
    }
    Ok((current, lhs))
}

The nom crate conveniently provides a peek combinator for parsing a token without consuming it. This allows my parser to lookahead at the next token and reason about operator precedence before continuing to parse an expression.

Before recursing into expr(code: Span) we also stored our precedence state so we can restore it later. This is because the call to expr consumes our input and the input returned will have an incorrect precedence for the current scope we are in. So the solution, is to store our precedence so we can restore it after expr(code: Span) returns.

We also define a function to return a precedence score for each operator we encounter. The specific numbers don’t matter as long as the comparisons yield the results we want.

pub fn precedence_for(op: &str) -> u32 {
    match op {
        " && " | " || " => 1,
        " == " | " != " | " IN " | " > " | " < " | " >= " | " <= " => 2,
        " + " => 3,
        _ => 0,
    }
}

And with that relatively simple implementation of precedence climbing, we have a correct expression parser!

Now when we can go and try to parse an expression like op1 == '000' && CRn == '0111' we get an AST that follows the proper operator precedence and therefore, allows to correctly reason about boolean expression and determine what the result would be given a concrete value for any identifiers like op1 and CRn.

Thanks for following along, and if you’re curious to take a deeper look at the underlying code mentioned in this post, feel free to check out the full source on my GitHub!